Propagating Compation Bands in Porous Media

All classes

Typical compaction patterns emanating from a uniaxially loaded confined two-dimensional structured porous media, here with a solid area fraction of $\phi = 0.40$:

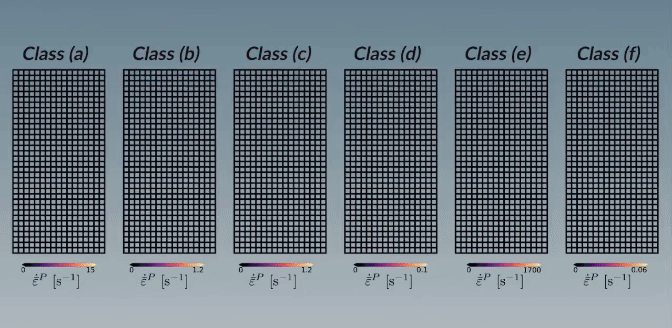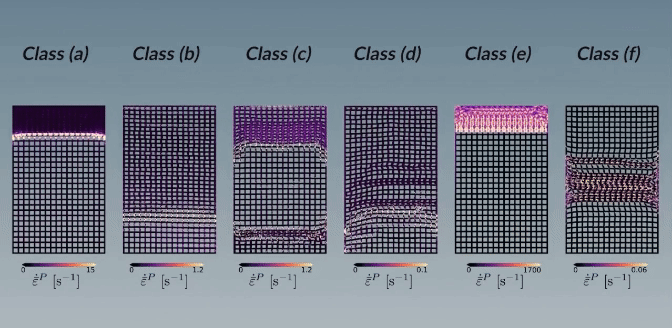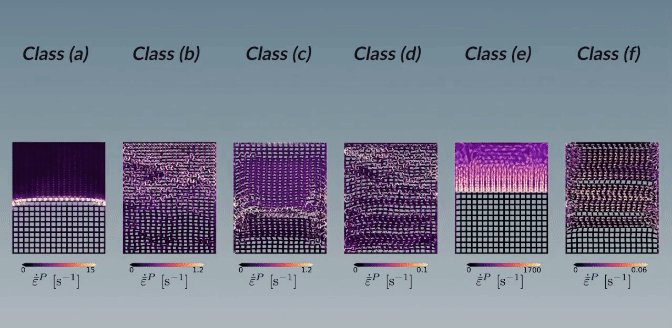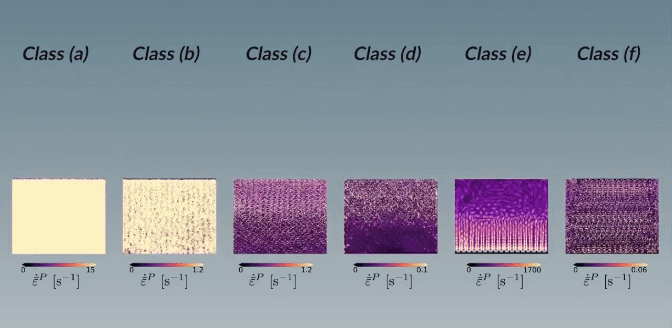
The structures are colored according to the plastic Hencky strain rate. The following parameters are used to get the various patterns:
(a) $S = 4 \cdot 10^{−3}, R = 10^{−5}$
(b) $S = 4 \cdot 10^{−3}, R = 4 \cdot 10^{−4}$
(c) $S = 4 \cdot 10^{−2}, R = 2 \cdot 10^{−2}$
(d) $S = 1.32 \cdot 10^{−3}, R = 4 \cdot 10^{−3}$
(e) $S = 10^{−1}, R = 10^{−5}$
(f) $S = 4 \cdot 10^{−3}, R = 10^{−1}$
Download full-resolution video here

Three-dimensional open-cell structure

While the above video shows two-dimensional structures, the same can be obtained with three-dimensional structures. Below is an example of an open-cell structure.

Here, $S = 10^{−2}, R = 10^{−3}$

More details

Read our full paper: Microstructural origin of propagating compaction patterns in porous media
by L. Blatny, P. Berclaz, F. Guillard, I. Einav and J. Gaume
published in Physical Review Letters, vol. 128 (2022)
Download supplemental document here
This work was featured in Physics Magazine

Contact: Lars Blatny